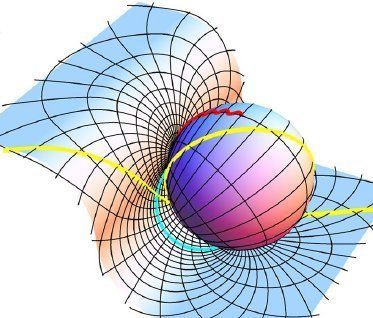
When saying the word geometry, most people think of the Euclidean kind, though in truth, this is only one half of the story. Geometry -our tool for describing our surrounding space- as a definition is not set in stone, it changes depending on how it will facilitate some calculations. In galaxies far far away, beings with other stimulations and environments, may have developed other versions of non- Euclidean geometry, maybe even one existing in four dimensions. As such, there is no correct form of geometry, just the best one for the occasion.
With that in mind, let’s see an occasion, where a non- Euclidean geometry is more convenient.
Ιn “Elements”, Euclid makes 5 assumptions and accepts them as truthful:
- A line can be drawn from every point to another different point
- A finite line can be extended indefinitely and continuously
- We can draw a circle with any central point and radius
- All right angles are equal
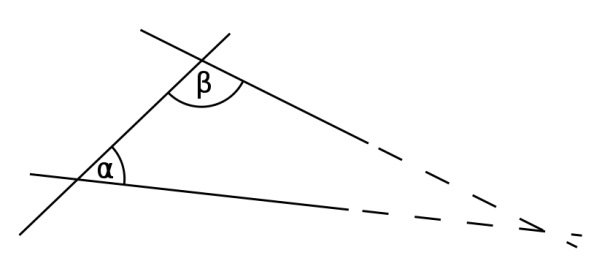
- If a line crosses two other lines to form two angles, who are on the same side of the first line and in between the other two, the two latter lines, if extended, will meet on the side on which they form the angles, that are less than two right angles.
Each of the postulates (assumptions) is in line with what we instinctually see, however with the passing of time, many mathematicians concluded that the fifth assumption can be extrapolated as a theorem from the other 4. Proving it was a different story, since no one ever managed it. One certain person, Giovanni Girolamo during his tries, came very close to discovering non- Euclidean geometry before its time.
Around 1823 to 1825, Nikolai Lobachevsky, during his try to prove the dependence of the fifth theorem to the other four, turned his attention to a new kind of geometry, that would replace the fifth assumption. His solution was the following axiom (assumption):
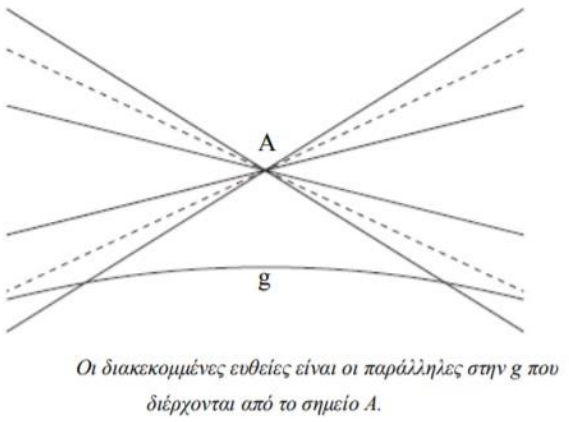
Lobachevsky axiom: There is a line, g, and a point A, such that two other lines can cross A and be on the same surface as g without intersecting.
This ingenious idea opened up a whole new way of understanding space.
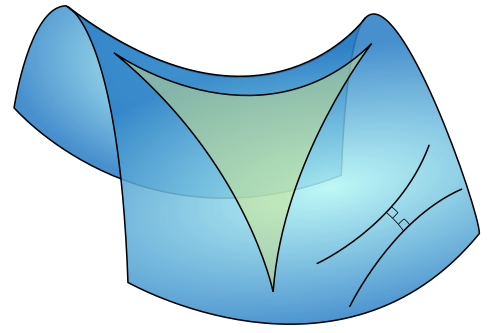
Another thing that is taken for granted and goes against everything we can conceive in Lobachevskian geometry- or otherwise called, hyperbolic geometry- is that the sum of the 3 angles of a triangle is less than two right angles or 180 degrees.
If one is on his road to understanding special relativity, he has become acquainted with Mikowski spaces. A Mikowski-an space is a flat four-dimensional space (lack-of-gravity wise) that constitutes the main tool for describing special relativity.
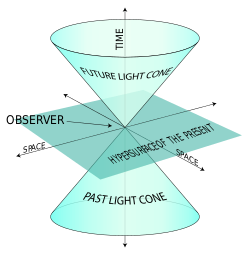
In short, in Mikowski space-time we can represent the action of light signals, via light cones. Since four dimensions cannot be transcribed in paper, we represent space in two axes (the horizontal ones) and time in one axis (the perpendicular/vertical).
The deviation to the subject of Mikowski spaces was not random, as they are a perfect application of hyperbolic geometry.
Lastly, that is not the only hyperbolic geometry that can describe and predict our cosmos. There is also elliptical geometry, a subject matter for another article.
Translation: Dimitrios Mataragkas
Proof-reading: Zoi Filiou