Η γεωμετρία είναι συνώνυμο της Ευκλείδειας γεωμετρίας, σωστά;
Οι περισσότεροι θα απαντούσαν καταφατικά, αλλά στην πραγματικότητα, αυτή είναι η μισή αλήθεια.
Η γεωμετρία, δηλαδή ο τρόπος με τον οποίο περιγράφουμε τον χώρο γύρω μας, δεν είναι μονοσήμαντα ορισμένη· είναι κατασκευασμένη με τέτοιο τρόπο ώστε να μας είναι πιο βολική η χρήση της. Όντας σε κάποιον μακρινό γαλαξία ή σε ένα παράλληλο σύμπαν, που έχουν ακολουθήσει διαφορετικές νοητικές διαδικασίες και έχουν δεχτεί άλλα ερεθίσματα, θα έχουν καταλήξει σε μη ευκλείδειες γεωμετρίες, ίσως και τετραδιάστατες, για να περιγράψουν το περιβάλλον τους. Δεν υπάρχει πιο «σωστή» γεωμετρία, μόνο πιο εύχρηστη.
Κρατώντας αυτές τις σκέψεις, ας δούμε μια συγκεκριμένη περίπτωση μη ευκλείδειας γεωμετρίας.
Από τα πρώτα μας σχολικά χρόνια ερχόμαστε σε επαφή με τα αξιώματα που όρισε ο Ευκλείδης, ούτως ώστε να θεμελιώσει την γεωμετρία του.
Τα γνωστά αιτήματα του Ευκλείδη, όπως αυτά παρουσιάζονται στα «Στοιχεία», είναι:
- Μπορούμε να φέρουμε μια ευθεία γραμμή από οποιοδήποτε σημείο προς οποιοδήποτε σημείο.
- Κάθε πεπερασμένη ευθεία μπορεί να προεκτείνεται συνεχώς και ευθυγράμμως.
- Μπορούμε να γράψουμε έναν κύκλο με οποιοδήποτε κέντρο και ακτίνα.
- Όλες οι ορθές γωνίες είναι ίσες.
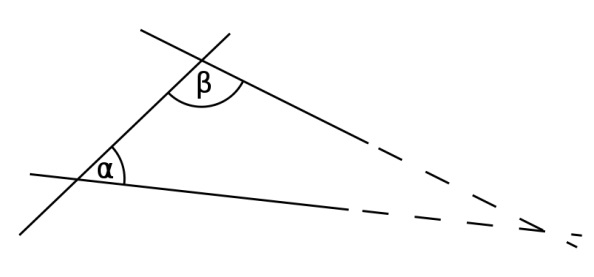
Αν μια ευθεία που τέμνει άλλες δύο ευθείες γραμμές σχηματίζει εντός και επί τα αυτά γωνίες με συνολικό άθροισμα μικρότερο από δύο ορθές, οι εν λόγω ευθείες, προεκτεινόμενες απεριόριστα, συναντώνται σε εκείνη τη μεριά όπου σχηματίζονται οι γωνίες που είναι λιγότερες από δύο ορθές.
Όλα αυτά τα αιτήματα είναι απόλυτα συμβατά με τη διαίσθησή μας, ωστόσο, ανά το πέρας των αιώνων, πολλοί μαθηματικοί θεώρησαν ότι το πέμπτο αξίωμα, όντας πιο περίπλοκο από τα υπόλοιπα, θα μπορούσε να εξαχθεί ως θεώρημα από τα πρώτα 4 αξιώματα.
Αυτό το εγχείρημα, σε πρώτη ανάλυση, απεδείχθη άκαρπο, μιας και κανείς δεν κατάφερε να αποδείξει ότι το 5ο αίτημα ήταν εξαρτημένο από τα άλλα 4. Ωστόσο, ο Giovanni Girolamo Saccheri, στην προσπάθειά του να το αποδείξει, ήρθε πολύ κοντά στην ανακάλυψη της μη ευκλείδειας γεωμετρίας έναν αιώνα νωρίτερα από την οριστική της ανακάλυψη.
Ο Nikolai Lobachevsky, στα 1823-1825, κατά την προσπάθειά του να αποδείξει την εξάρτηση του πέμπτου αιτήματος του Ευκλείδη από τα άλλα 4, έστρεψε την προσοχή του σε ένα νέο είδος γεωμετρίας, το οποίο αντικατέστησε το αίτημα της παραλληλίας (το 5ο ευκλείδειο αξίωμα) με το ακόλουθο:
Αξίωμα Lobachevsky:
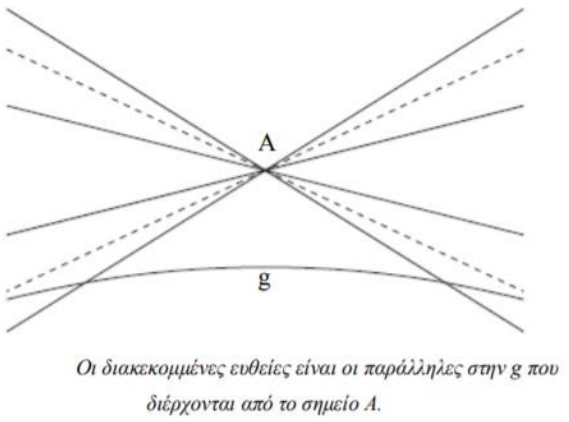
Υπάρχει ευθεία g και σημείο A εκτός αυτής, έτσι ώστε από το A να διέρχονται τουλάχιστον δύο ευθείες που βρίσκονται στο ίδιο επίπεδο με την g και δεν την τέμνουν.
Η ριζοσπαστική ιδέα του Lobachevsky να αντικαταστήσει το 5ο αξίωμα του Ευκλείδη, το οποίο ήταν αδύνατο να παραχθεί από τα 4 πρώτα αιτήματα, με την υπόθεση του αντίθετου του αξιώματος, άνοιξε έναν ολοκαίνουριο δρόμο στην κατανόηση που έχουμε για τον χώρο.
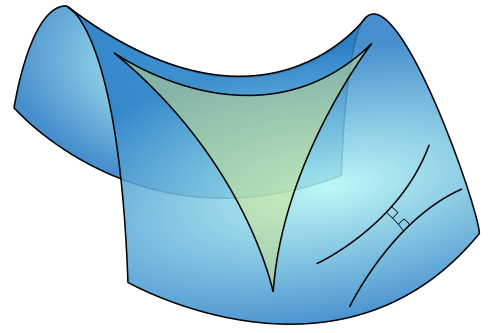
Μια ακόμα πρόταση που έρχεται σε αντιδιαστολή με την αντίληψη που έχουμε για τον χώρο είναι ότι σε ένα τρίγωνο της γεωμετρίας Lobachevsky, γνωστής και ως υπερβολικής γεωμετρίας, το άθροισμα των γωνιών του είναι μικρότερο από δύο ορθές.
Όποιος έχει κάνει τα πρώτα του βήματα προς την κατανόηση της ειδικής θεωρίας της σχετικότητας είναι κάπως εξοικειωμένος με τον χωρόχρονο Minkowski, δηλαδή με τον επίπεδο (επίπεδο υπό την έννοια της απουσίας βαρύτητας) τετραδιάστατο χώρο, εντός του οποίου μπορεί να περιγραφεί με τον πλέον κατάλληλο τρόπο η ειδική θεωρία της σχετικότητας.

Πολύ περιεκτικά, στον χωρόχρονο Minkowski, μπορούμε να αναπαραστήσουμε τις χωροχρονικές εξελίξεις φωτεινών σημάτων χρησιμοποιώντας κώνους φωτός (βλέπε διπλανό σχήμα). Μιας και είναι αδύνατη η ταυτόχρονη γραφική αναπαράσταση και των τεσσάρων διαστάσεων, στους κώνους φωτός χρησιμοποιούμε δύο χωρικούς άξονες (τους οριζόντιους) και έναν χρονικό (τον κάθετο).
Αυτή η παρέκκλιση από το θέμα μας δεν έγινε τυχαία, μιας και ο χωρόχρονος Minkowski αποτελεί μια άριστη εφαρμογή της υπερβολικής γεωμετρίας στη μελέτη φυσικών συστημάτων.
Βέβαια, αυτή δεν είναι η μοναδική μη ευκλείδεια γεωμετρία ικανή να περιγράψει τον κόσμο μας· μάλιστα, έχει ανακαλυφθεί κιόλας ακόμη μία, η ελλειπτική γεωμετρία! Και αυτή, όπως η υπερβολική, έχει τα ιδιαίτερα γνωρίσματά της, τα οποία μπορούμε να δούμε σε επόμενο άρθρο.
